贝塞尔曲线原理介绍及基础使用

贝塞尔曲线概述

贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。
贝塞尔曲线主要用于二维图形应用程序中的数学曲线，曲线由起始点，终止点（也称锚点）和控制点组成，通过调整控制点，贝塞尔曲线的形状会发生变化。
在计算机图形学中贝赛尔曲线的运用很广泛，例如Photoshop中的钢笔效果，Flash5的贝塞尔曲线工具，在软件GUI开发中一般也会提供对应的方法来实现贝赛尔曲线。

认识贝塞尔曲线

以下公式中：B(t)为t时间下点的坐标；P0为起点,Pn为终点,Pi为控制点

一阶贝塞尔曲线（直线）

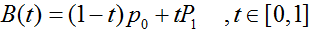
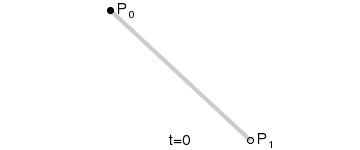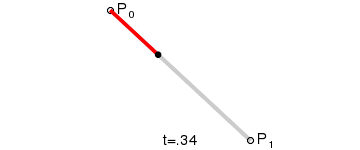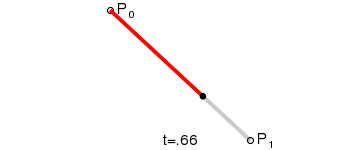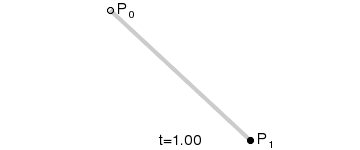
二阶贝塞尔曲线（抛物线）

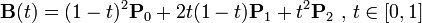
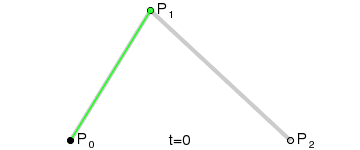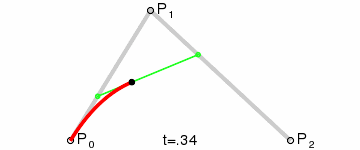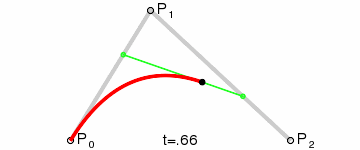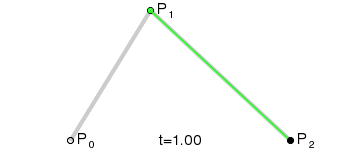
三阶贝塞尔曲线

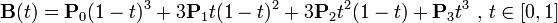
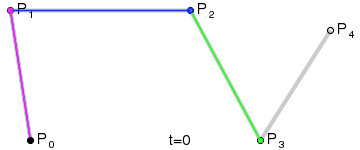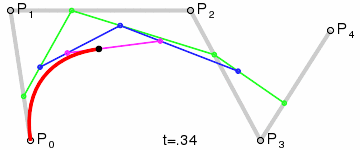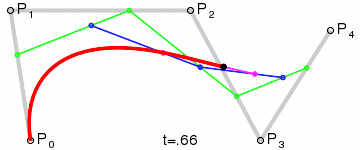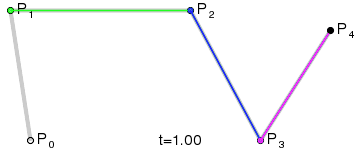
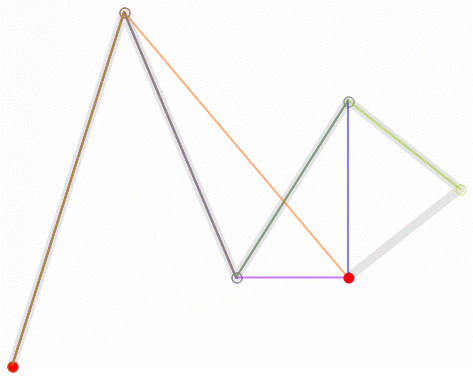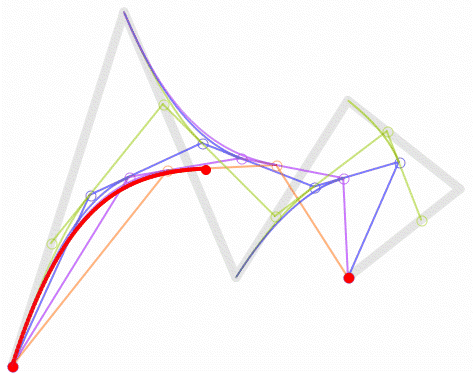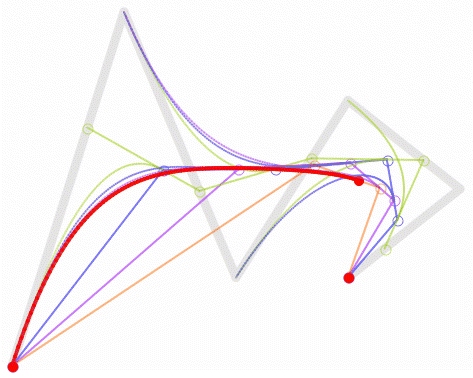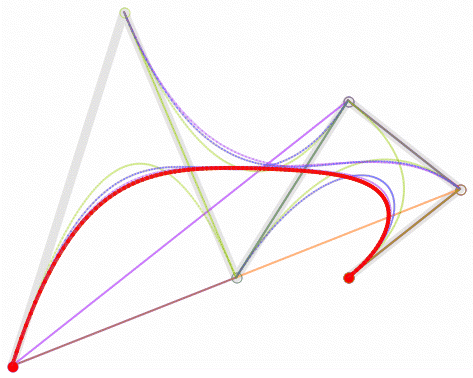
高阶贝塞尔曲线

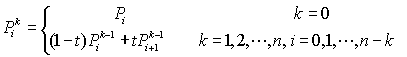
四阶贝塞尔曲线

五阶贝塞尔曲线

Android中的贝塞尔曲线

Android从API1起就支持了贝塞尔曲线，实现方式是借助android.graphics.Path类。

Path.moveTo(float x, float y) // Path的初始点
Path.lineTo(float x, float y) // 线性公式的贝赛尔曲线
Path.quadTo(float x1, float y1, float x2, float y2) // 二次方公式的贝赛尔曲线
Path.cubicTo(float x1, float y1, float x2, float y2, float x3, float y3) // 三次方公式的贝赛尔曲线

贝塞尔曲线基础使用

现在绘制一条基础的贝塞尔曲线。自定义一个用来绘制贝塞尔曲线的View，在View的onDraw方法中实现以下代码:

@Override
protected void onDraw(Canvas canvas) {
    super.onDraw(canvas);

    mPath.moveTo(100, 100);
    mPath.cubicTo(800, 100, 100, 800, 800, 800);
    // 一共四个点，(100, 100)和(800, 800)分别为起点和终点,(800, 100)和(100, 800)为操作点

    canvas.drawPath(mPath, mPaint);
}

实现效果如下：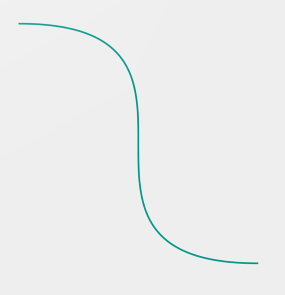

贝塞尔曲线实例

手机QQ可以发短视频，短视频消息在消息界面中的显示效果如下：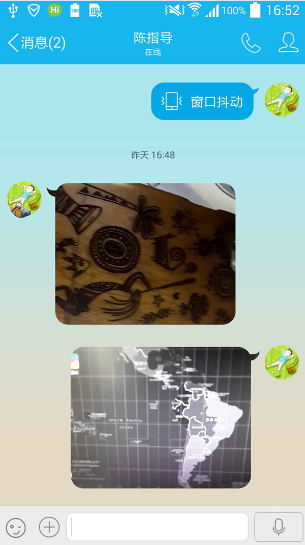

可以看到，气泡的左上角或右上角有一个用曲线绘制出来的小勾。很明显，这个小勾就是用贝塞尔曲线绘制出来的。我们如果也要做一个这样的效果，应该怎么办呢？

三角形初级气泡

主要原理是将原图作为BitmapShader，关联到Paint对象上，然后用这个Paint去绘制整个图形。
流程分为两步：

1. 裁圆角矩形，注意，矩形的宽度是原图的宽度减去三角形水平的宽度。
2. 绘制三角形

代码如下：

public static Bitmap processImage(Bitmap bitmap) {
    Bitmap bmp = Bitmap.createBitmap(bitmap.getWidth(), bitmap.getHeight(), Bitmap.Config.ARGB_8888);
    BitmapShader shader = new BitmapShader(bitmap, BitmapShader.TileMode.CLAMP, BitmapShader.TileMode.CLAMP);

    int width = bitmap.getWidth();
    int height = bitmap.getHeight();

    Canvas canvas = new Canvas(bmp);
    Paint paint = new Paint();
    paint.setAntiAlias(true);
    paint.setShader(shader);

	// 1.裁圆角，目标区域的宽度等于原图的宽度减去三角形的宽度
	RectF rect = new RectF(0, 0, width - TRIANGLE_WIDTH, height);
	canvas.drawRoundRect(rect, RADIUS, RADIUS, paint);

	// 2.绘制三角
	Path triangle = new Path();
	triangle.moveTo(width, TRIANGLE_OFFSET);
	triangle.lineTo(width - TRIANGLE_WIDTH, TRIANGLE_OFFSET - TRIANGLE_HEIGHT / 2);
	triangle.lineTo(width - TRIANGLE_WIDTH, TRIANGLE_OFFSET + (TRIANGLE_HEIGHT / 2));
	triangle.close();

	canvas.drawPath(triangle, paint);

	return bmp;
}

绘制的效果如下：

贝塞尔气泡

上文已经阐述过贝塞尔曲线的原理了，这边给出了一个基础的气泡设计图，很粗糙。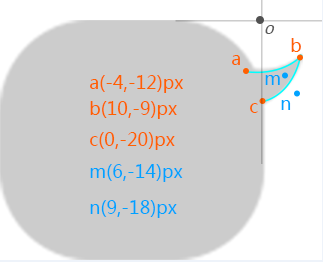

有了这个图，我们就可以按照图中提供的坐标去绘制整个贝塞尔气泡了。（注意，由于原图比较大，代码绘制过程中，坐标根据设计图中的坐标乘以了3）

public static final int dp2px(float dp, Resources res) {
        return (int) (dp * res.getDisplayMetrics().density + 0.5f);
}

public static Bitmap processImageWithBezier(Bitmap bitmap, Resources res) {
	Bitmap bmp = Bitmap.createBitmap(bitmap.getWidth(), bitmap.getHeight(), Bitmap.Config.ARGB_8888);
	BitmapShader shader = new BitmapShader(bitmap, BitmapShader.TileMode.CLAMP, BitmapShader.TileMode.CLAMP);

	int w = bitmap.getWidth();
	int h = bitmap.getHeight();

	Canvas canvas = new Canvas(bmp);
	Paint paint = new Paint();
	paint.setAntiAlias(true);
	paint.setShader(shader);

	// 1.裁圆角，目标区域的宽度等于原图的宽度减去三角形的宽度
	RectF rect = new RectF(0, 0, w - TRIANGLE_WIDTH, h);
	canvas.drawRoundRect(rect, RADIUS, RADIUS, paint);

	// 2.绘制圆角
	float startX, startY;
	float controlX1, controlY1;
	float endX1, endY1;

	float controlX2, controlY2;
	float endX2, endY2;

	Path path = new Path();

	// a->b
	startX = w - dp2px(42f, res);
	startY = dp2px(36f, res);
	path.moveTo(startX, startY);
	endX1 = w;
	endY1 = dp2px(27f, res);
	controlX1 = w - dp2px(12f, res);
	controlY1 = dp2px(42f, res);
	path.quadTo(controlX1, controlY1, endX1, endY1);

	// b->c
	endX2 = w - dp2px(30, res);
	endY2 = dp2px(60f, res);
	controlX2 = w - dp2px(3f, res);
	controlY2 = dp2px(58f, res);
	path.quadTo(controlX2, controlY2, endX2, endY2);

	path.close();

	canvas.drawPath(path, paint);

	return bmp;
}

绘制的效果如下：

总结

本文介绍了贝塞尔曲线的原理以及其基础应用。显然，贝塞尔曲线可以用的地方很多很多，可以用来实现十分精美的动画，比如手机QQ消息列表的红点消除拖动动画等。
本文代码见BezierDemo